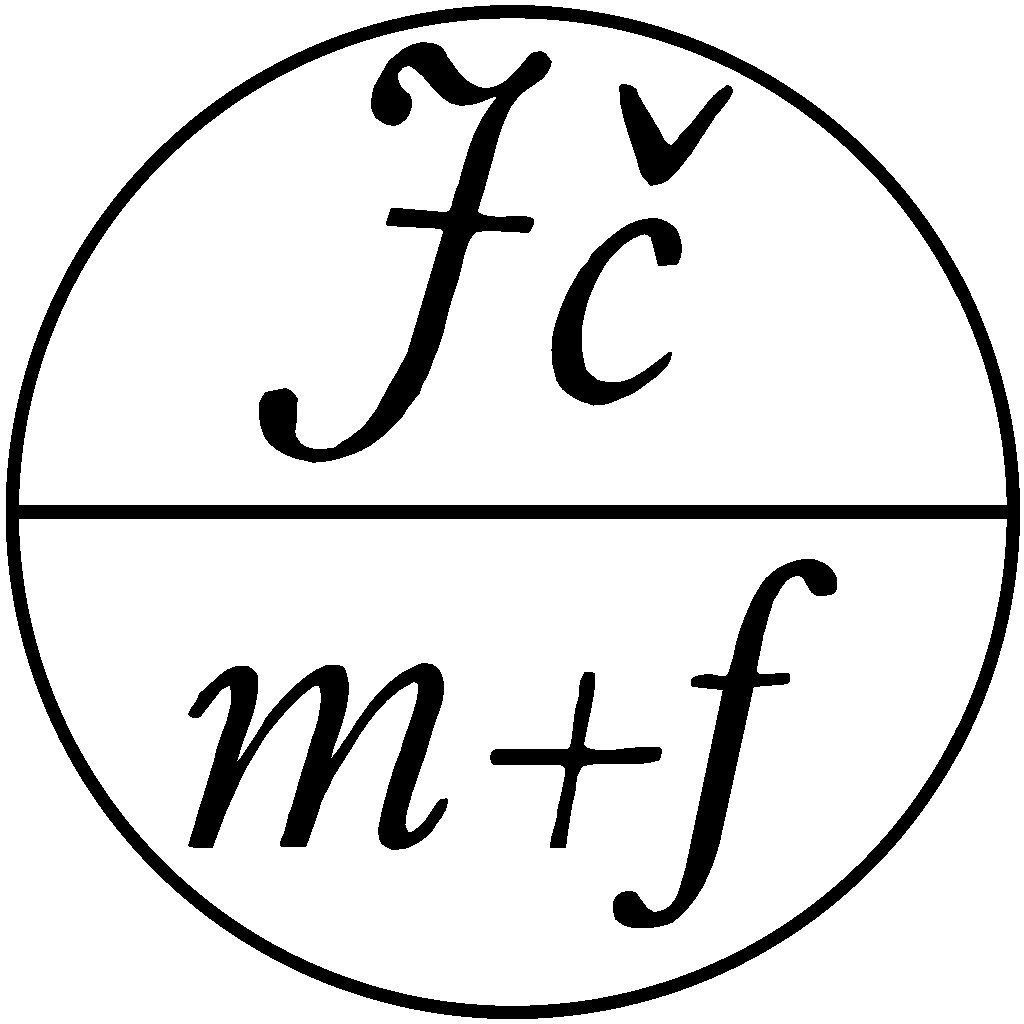Aritmetický průměr posloupnosti
Abstrakt
Článek ze série věnované úlohám matematické olympiády – kategorie P (programování) diskutuje různé možnosti řešení jedné soutěžní úlohy krajského kola ze školního roku 2013/14. Úkolem je nalézt v posloupnosti čísel co nejdelší souvislý úsek, jehož aritmetický průměr je roven zadané hodnotě. Článek demonstruje různé programátorské postupy, které lze využít pro zvýšení časové efektivity řešení, jako jsou předvýpočet, prefixové součty posloupnosti nebo vhodně seřazení dat. Kromě detailního rozboru úlohy najdeme v článku tři základní varianty řešení zapsané i ve formě ukázkového programu.Stahování
Publikováno
Jak citovat
Číslo
Sekce
Licence
Autoři, kteří publikují v tomto časopise, souhlasí s následujícími body:
- Autoři si ponechávají copyright a garantují časopisu právo prvního publikování, přitom je práce zároveň licencována pod Creative Commons Attribution licencí, která umožňuje ostatním sdílet tuto práci s tím, že přiznají jejího autora a první publikování v tomto časopisu.
- Autoři mohou vstupovat do dalších samostatných smluvních dohod pro neexkluzivní šíření práce ve verzi, ve které byla publikována v časopise (například publikovat ji v knize), avšak s tím, že přiznají její první publikování v tomto časopisu.

Obsah časopisu podléhá licenci Creative Commons Uveďte autora 3.0 Česko